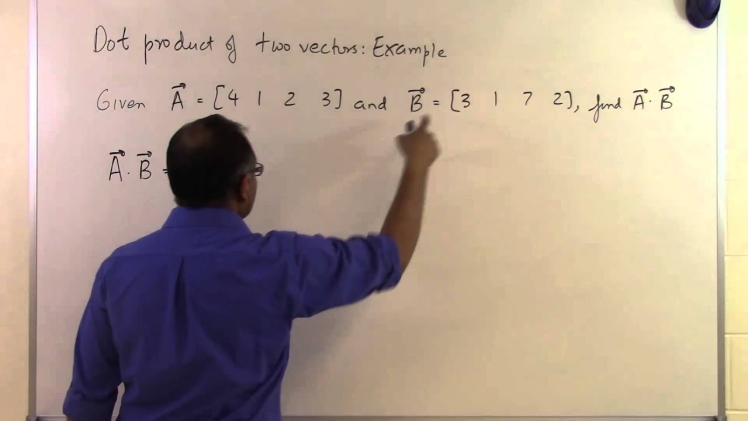A dot product consists mainly of two vectors. It is a projection of one vector to another vector. For example, we have two vectors ‘x’ and ‘y’ pointing out in the same direction. We need to find out how much of the vector ‘x’ is pointing out in the direction of the vector ‘y’. This is based on a quantity where it is positive if both the vectors ‘x’ and ‘y’ point out in the same direction, would be zero if they are perpendicular to each other and negative if they point in different directions. The dot product is generally a multiplication of vectors where the result is a scalar one.
Explanation of a dot product with an example
So the question lies that how much of the vector ‘x’ is pointing towards the same direction as vector ‘y’. Thus, we don’t have to rely on its magnitude or length, we just need the direction of it. So let us avoid the length of ‘y’ and denote the vector as one unit. Hypothetically, we replace ‘y’ with a unit vector that is pointing in the same direction as ‘y’. We name this vector ‘u’. Then the formula looks like u=y/|y|.
So, the dot product of ‘x’ with unit vector ‘u’ can be denoted as x.u which is defined as the projection of the ‘x’ vector in the direction or line of the ‘u’ vector. This can also be placed as the quantity of the ‘x’ vector that is pointing in the direction of the ‘u’ vector or the unit vector. Let us think for an instance that both the ‘x’ and ‘u’ vectors are pointing towards the same direction. Then we can foretell that x.u is the length or the magnitude of the shadow of ‘x’ falling on the ‘u’ vector as they are facing the same direction and the light source is directly perpendicular to the ‘u’ vector. Thus a right-angled triangle is formed with vector ‘x’ and the shadow and we can place the equation as x.u=|x|cosΘ. Here Θ is the angle formed between vector ‘x’ and vector ‘y’.
Thus, if vectors ‘x’ and ‘u’ were perpendicular then no shadow would have been cast. Then the value would be cosΘ=cosπ/2=0 and the dot product x.u would be 0. Therefore, if the angle between ‘x’ and ’u’ were much greater than π/2, then the reflection would not reach ‘u’. Thus, the dot product x.u is negative since cosΘ is less than zero.
So now, if we take in vector ‘y’ which is not of unit one, then the dot product x.y would consist of the magnitude of both the vectors |x| and |y|. Hence, if we go by the formula of u=y/|y|, then the dot product x.y will look like x.y=|x| |y|cosΘ.
Conclusion
To conclude, a dot product is always a multiplication of two vectors where one vector is projected over the other vector. Moreover, including all the mathematical calculations, a dot product should have a scalar quantity. Vectors are generally categorized into two forms. One is called a dot product which is a scalar quantity and the other is a cross-product which is a vector quantity. There are many more definitions related to dot products such as geometric and algebraic. The dot product also has many properties that are categorized as Cumulative property, Distributive property, Scalar Property, Bilinear property, and so on.
Thus, to get a complete view of all the properties and the basic fundamentals of the dot product, you can visit Cuemath for essential information. You can book a session regarding your math program and the teachers here are eager to help. So, do visit and experience the benefits of our online math classes at Cuemath.